Talk:Möbius strip
| Möbius strip has been listed as one of the Mathematics good articles under the good article criteria. If you can improve it further, please do so. If it no longer meets these criteria, you can reassess it. | |||||||||||||
| |||||||||||||
A fact from this article appeared on Wikipedia's Main Page in the "Did you know?" column on May 3, 2022. The text of the entry was: Did you know ... that the recycling symbol (pictured) depicts a Möbius strip? | |||||||||||||
| Current status: Good article | |||||||||||||
| This is the talk page for discussing improvements to the Möbius strip article. This is not a forum for general discussion of the article's subject. |
Article policies
|
| Find sources: Google (books · news · scholar · free images · WP refs) · FENS · JSTOR · TWL |
| Archives: 1, 2Auto-archiving period: 12 months |
| This It is of interest to the following WikiProjects: | |||||||||||
| |||||||||||
|
This page has archives. Sections older than 365 days may be automatically archived by Lowercase sigmabot III when more than 5 sections are present. |
Twice cut strip
[edit]Wouldn't that create two Möbius strips instead? Explanation caption for the image lists that it creates a Möbius strip with two tracks, and one non Möbius strip. In reality, this should create a two tracked Möbius strip and a separate Möbius strip. Cmdrscotty (talk) 14:21, 1 September 2020 (UTC)
- The pink/blue strip has two sides and is not a Möbiusstrip. --Ag2gaeh (talk) 16:41, 1 September 2020 (UTC)
Did you know nomination
[edit]As for ALT1 below. Aion is NOT holding a Möbius strip. Give me a break and take a better look. It is just a strip and the Romans perished (due to lead poisoning) before even inventing zero. — Preceding unsigned comment added by 2A02:2168:B03:3F14:0:0:0:4 (talk) 12:42, 23 August 2024 (UTC)
- The following is an archived discussion of the DYK nomination of the article below. Please do not modify this page. Subsequent comments should be made on the appropriate discussion page (such as this nomination's talk page, the article's talk page or Wikipedia talk:Did you know), unless there is consensus to re-open the discussion at this page. No further edits should be made to this page.
The result was: promoted by Kingsif (talk) 10:41, 23 April 2022 (UTC)
- ... that the recycling symbol (pictured) depicts a Möbius strip? Source: https://books.google.com/books?id=RMH2DwAAQBAJ&pg=PA31

- ALT1: ... that the Möbius strip can be seen on ancient Roman mosaics (pictured)? Source: https://www.jstor.org/stable/27843983 and https://arxiv.org/abs/1609.07779
- ALT2: ... that Parisian seamstresses initiated novices by making them sew a Möbius strip collar onto a garment? Source: https://www.jstor.org/stable/27843983
- ALT3: ... that the Möbius strip has been used to shape bagels, bacon, and pasta? Source: Bagels: https://www.npr.org/sections/thesalt/2015/08/06/429437860/cut-your-bagel-the-mathematically-correct-way – Bacon: https://www.theverge.com/2014/9/5/6110563/mobius-bacon-recipe – Pasta: https://www.nytimes.com/2012/01/10/science/pasta-inspires-scientists-to-use-their-noodle.html
- ALT4: ... that the Möbius strip can be made to have a perfectly circular boundary (pictured)? Source: https://vimeo.com/286360639
- ALT5: ... that the Möbius strip stays in one piece when cut along its centerline (pictured)? Source: https://books.google.com/books?id=IwDvAAAAMAAJ&pg=PA53
- ALT6: ... that the Möbius strip can have two sides in non-Euclidean spaces? Source: https://www.jstor.org/stable/3026946
- Reviewed: Template:Did you know nominations/Frequency modulation encoding
Improved to Good Article status by David Eppstein (talk). Self-nominated at 18:14, 18 April 2022 (UTC).
 Article has achieved Good Article status. No issues of copyvio or plagiarism. All sources appear reliable. QPQ is done. Hooks are interesting and sourced. Are there any other images you would like to include in the nomination? There are some cool ones in commons, but I guess new hooks would have to be created to use some of them. Thriley (talk) 02:33, 19 April 2022 (UTC)
Article has achieved Good Article status. No issues of copyvio or plagiarism. All sources appear reliable. QPQ is done. Hooks are interesting and sourced. Are there any other images you would like to include in the nomination? There are some cool ones in commons, but I guess new hooks would have to be created to use some of them. Thriley (talk) 02:33, 19 April 2022 (UTC)
- I added three more for some of the other hooks. Not sure the mosaic one works at DYK thumbnail size though. —David Eppstein (talk) 05:02, 19 April 2022 (UTC)
- You are right, the mosaic wouldn't work. Shame about that. The others look good. Thriley (talk) 17:02, 19 April 2022 (UTC)
- Promoter comment: taking the recycling logo because I can image lots of people will be trying to work it out and surprised to learn because that logo is so commonplace. Kingsif (talk) 10:41, 23 April 2022 (UTC)
- You are right, the mosaic wouldn't work. Shame about that. The others look good. Thriley (talk) 17:02, 19 April 2022 (UTC)
- I added three more for some of the other hooks. Not sure the mosaic one works at DYK thumbnail size though. —David Eppstein (talk) 05:02, 19 April 2022 (UTC)
Mobius M. Mobius
[edit]Should Mobius M. Mobius be included in the popular culture section? (Sources: 1, 2, 3, 4, 5) Sahaib (talk) 17:35, 3 May 2022 (UTC)
- I'm leaning towards no. If the connection is only to the misspelled name "Mobius", no. If we have in-depth published reliable sources specifically connecting this character's plot line to the Möbius strip itself, and not just fan speculation which some of your sources look like, and this plot line is the main point of a movie about this character, then maybe it could be listed among other fictional works with Möbius-strip plotlines. Or if your links' theory that this is another example of the bullshit "Möbius strips are things we don't understand therefore they could cause time loops" trope turns out to be validated, then maybe it could be mentioned, briefly, in the sentence with three examples of this trope. But the current Wikipedia article Mobius M. Mobius contains no content that would make a significant enough connection to this article to link to. The popular culture section is not intended as a catch-all listing of anything vaguely related (go to tvtropes for that sort of thing), but as an organized survey of different wide areas of popular culture to which the idea of a Möbius strip has had a significant influence (fine art, design, literature, etc). A name of a character in a movie franchise is not a significant influence to a wide area of popular culture. We already have plenty of examples of movies where the strip plays a much more significant role in the overall structure of the movie and not just in the names or behavior of one its characters. —David Eppstein (talk) 17:43, 3 May 2022 (UTC)
Area of swept surface
[edit]It might be interesting to say what the area of the surface swept by a rotating line segment is. I don't know the answer, but I found a reference saying what the area isn't: it isn't what you would get by trying to apply Pappus's centroid theorem. The rotation makes it sweep out a bigger area than a non-rotating segment would. See the last line of:
- Goodman, A. W.; Goodman, Gary (1969), "Generalizations of the theorems of Pappus", The American Mathematical Monthly, 76: 355–366, doi:10.1080/00029890.1969.12000217, JSTOR 2316426, MR 0240702
—David Eppstein (talk) 01:21, 4 May 2022 (UTC)
- Interesting. Numerically (from their formula) it's ≈6.62715 for a fairly natural choice of dimensions, namely a strip width of 1 unit rotating while following a circle of radius 1, indeed slightly greater than Pappus's theorem's estimate of 2π. I searched for that constant (and approximations) and couldn't find anything, which is a crude way of going about things, but I'd find it highly unlikely that someone would evaluate the area analytically and not put a numerical value to it. So I suspect it's not been properly investigated, and I doubt there's a closed form. For posterity, the integral is . Ovinus (talk) 03:26, 9 May 2022 (UTC)
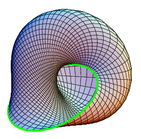
Relation to Umbilic torus
[edit]The link to "Umbilic torus" in the "See also" section is accompanied with a claim that the Umbilic torus can be obtained from a Möbius strip by gluing the latter along its single edge. IMHO, that statement is false, at least in regular 3D space, where the result would have to be a self-intersecting surface, assuming that the gluing is performed in the 3D space, rather than through some topological magic (sorry, I am not an expert in this field and lack the right terminology; my judgements are restricted to common sense intuition). Note that the article about the umbilic torus doesn't establish any relation of it with the Möbius strip (the link in the "See also" section doesn't count as such). I think that the misleading sentence has to be either removed or reformulated in a less confusing way and a more detailed explanation can be provided in the article about umbilic torus. Leon.Manukyan (talk) 08:41, 23 September 2023 (UTC)
- You are confusing the standard embedding of the Möbius strip (with one half-twist) with the Möbius strip itself (a topological surface independent of how it is embedded into space). If you perform any odd number of half-twists to a strip before gluing it back to itself, you get a Möbius strip, with a different embedding for each different number of half-twists (see the second paragraph of the lead). The umbilic torus has a boundary that, if you cut along the ridges, is a Möbius strip. It is a Möbius strip embedded with three half-twists rather than one, but that is still a Möbius strip. —David Eppstein (talk) 10:15, 23 September 2023 (UTC)
- You provided the same justification in your reversal of my earlier edit. My feeling was that something was wrong with it. A Möbius strip is single-sided whereas the Umbilic torus apparently has inside and outside. Now thinking about it more carefully, I guess that I found the flaw in your reasoning. The fact that the boundary goes three times around the center of the torus doesn't mean that the strip makes three half-twists. Actually it only makes a full twist (two half-twists). Hence it is not topologically equivalent to a Möbius strip. Leon.Manukyan (talk) 10:31, 23 September 2023 (UTC)
- Ok, this time I think you may be correct. If it really were a Möbius strip then (regardless of number of twists) traveling around the boundary (without crossing any ridges) until you return to your start should take you to the inside, but it doesn't. —David Eppstein (talk) 11:53, 23 September 2023 (UTC)
- You provided the same justification in your reversal of my earlier edit. My feeling was that something was wrong with it. A Möbius strip is single-sided whereas the Umbilic torus apparently has inside and outside. Now thinking about it more carefully, I guess that I found the flaw in your reasoning. The fact that the boundary goes three times around the center of the torus doesn't mean that the strip makes three half-twists. Actually it only makes a full twist (two half-twists). Hence it is not topologically equivalent to a Möbius strip. Leon.Manukyan (talk) 10:31, 23 September 2023 (UTC)